BAB II
Penjelasan
Model Kurva
Kurva adalah garis dan ruas garis yang membentuk kurva – kurva sederhana. Kurva dapat digambarkan dengan bermacam – macam bentuk, bentuknya bisa teratur bisa juga tidak teratur.
Kurva dibagi menjadi beberapa contoh yaitu :
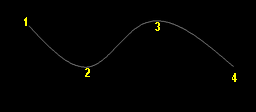
1. Kurva Spline
Sejarah
Sebelum komputer digunakan , perhitungan numerik dilakukan dengan tangan . Fungsi seperti fungsi langkah yang digunakan tetapi polinomial umumnya disukai . Dengan munculnya komputer , splines pertama diganti polinomial dalam interpolasi , dan kemudian disajikan dalam bentuk pembangunan halus dan fleksibel dalam komputer grafis .
Hal ini umumnya diterima bahwa referensi matematika pertama yang splines adalah 1.946 kertas dengan Schoenberg , yang mungkin adalah tempat pertama bahwa kata ” spline ” digunakan sehubungan dengan halus, piecewise polinomial pendekatan . Namun, ide ini berakar pada pesawat dan industri pembuatan kapal .
Dalam kata pengantar ( Bartels et al . , 1987) , Robin Forrest menjelaskan ” lofting ” , teknik yang digunakan dalam industri pesawat terbang Inggris selama Perang Dunia II untuk membangun template untuk pesawat terbang dengan melewati strip kayu tipis ( disebut ” splines ” ) melalui titik diletakkan di lantai loteng desain besar , teknik dipinjam dari desain kapal -hull .
Selama bertahun-tahun praktek desain kapal telah dipekerjakan untuk merancang model di kecil . Keberhasilan desain kemudian diplot pada kertas grafik dan poin-poin penting dari plot itu kembali diplot pada kertas grafik yang lebih besar untuk ukuran penuh . Strip kayu tipis memberikan interpolasi poin-poin penting dalam kurva halus . Strip akan diadakan di tempat pada titik-titik diskrit ( menggunakan beban memimpin , yang disebut ” bebek ” oleh Forrest (lihat Spline Ducks untuk ilustrasi ) ; Schoenberg digunakan ” anjing ” atau ” tikus ” ) dan antara titik-titik akan menganggap bentuk minimum energi regangan .
Menurut Forrest , satu dorongan yang mungkin untuk model matematis untuk proses ini adalah potensi kerugian dari desain komponen penting untuk seluruh pesawat harus loteng terkena bom musuh . Hal ini melahirkan ” kerucut lofting ” , yang digunakan irisan kerucut untuk memodelkan posisi kurva antara bebek .
Lofting kerucut digantikan oleh apa yang kita sebut splines pada awal tahun 1960 berdasarkan karya JC Ferguson di Boeing dan ( agak belakangan ) oleh MA Sabin di British Aircraft Corporation . Kata ” spline ” awalnya dalam dialek Anglia Timur .
Penggunaan splines untuk badan mobil model tampaknya memiliki beberapa awal independen. Kredit diklaim atas nama de Casteljau di Citroen , Pierre Bezier di Renault , dan Birkhoff , Garabedian , dan de Boor di General Motors (lihat Birkhoff dan de Boor , 1965) , semua untuk pekerjaan yang terjadi di tengah- awal 1960-an atau 1950-an. Setidaknya satu kertas de Casteljau itu diterbitkan, tetapi tidak banyak , pada tahun 1959 .Karya De Boor yang di General Motors menghasilkan sejumlah makalah yang diterbitkan pada awal tahun 1960 , termasuk beberapa pekerjaan fundamental di B - splines .
Pekerjaan juga sedang dilakukan di Pratt & Whitney Pesawat , di mana dua dari penulis pertama pengobatan buku - panjang splines ( Ahlberg et al , 1967. ) [ 13 ] dipekerjakan , dan David Taylor Model Basin , oleh Feodor Theilheimer . Pekerjaan di General Motors adalah rinci baik di Birkhoff ( 1990) dan Young ( 1997) . [ 14 ] Davis ( 1997) meringkas beberapa bahan ini .
Dalam matematika, sebuah spline adalah khusus fungsi didefinisikan piecewise oleh polinomial. Dalam interpolating masalah, spline interpolasi sering lebih suka polinomial interpolasi karena menghasilkan hasil yang sama, bahkan ketika menggunakan rendah derajat polinomial, sementara menghindari Runge's fenomena yang lebih tinggi derajat. Dalam ilmu computer subbidang dibantu komputer-komputer desain dan grafis, istilah “spline” lebih sering merujuk pada sebuah polynomial (parametrik) kurva. Dalam ilmu komputer subbidang yang dibantu komputer desain dan komputer grafis, istilah "spline" lebih sering merujuk pada sebuah piecewise polinomial (parametrik) Kurva. Kurva Splines populer dalam subbidang ini karena kesederhanaan konstruksi mereka, mereka kemudahan dan akurasi evaluasi, dan kapasitas mereka untuk perkiraan kompleks melalui pemasangan kurva bentuk dan desain kurva interaktif. Kurva Splines populer dalam Kesederhanaan subbidang konstruksi ini karena mereka, mereka Kemudahan dan akurasi evaluasi, dan kapasitas mereka untuk bentuk kompleks Perkiraan Kurva melalui pemasangan dan Kurva desain interaktif. Istilah spline berasal dari spline fleksibel perangkat yang digunakan oleh pembuat kapal dan draftsmen untuk menggambar bentuk halus. Berasal dari istilah spline spline fleksibel Perangkat yang Digunakan oleh pembuat kapal dan draftsmen untuk Menggambar bentuk halus. Istilah "spline" Digunakan untuk merujuk kepada berbagai kelas fungsi yang Digunakan dalam aplikasi yang Memerlukan interpolasi data dan / atau smoothing. Data dapat berupa satu dimensi atau multi-dimensi. Data dapat berupa satu dimensi atau multi-dimensi. Fungsi untuk interpolasi spline biasanya ditetapkan sebagai langkah yang tepat minimizers dari kekasaran (misalnya integral kuadrat kelengkungan) tunduk pada interpolasi kendala.Fungsi untuk interpolasi spline biasanya ditetapkan Sebagai langkah yang tepat minimizers dari kekasaran (Misalnya terpisahkan Kuadrat kelengkungan) tunduk pada interpolasi kendala. Splines smoothing dapat dipandang sebagai generalisasi dari interpolasi splines di mana fungsi ditentukan untuk memperkecil kombinasi yang berbobot rata-rata kuadrat kesalahan pendekatan di atas diamati data dan mengukur kekasaran. Merapikan Splines Sebagai Generalisasi dapat dipandang dari interpolasi splines di mana fungsi ditentukan untuk memperkecil Kombinasi yang berbobot rata-rata Pendekatan Kuadrat kesalahan data yang diamati di atas Mengukur dan kekasaran. Untuk sejumlah bermakna definisi dari kekasaran ukuran, fungsi spline ditemukan di alam dimensi terbatas, yang merupakan alasan utama mereka dalam perhitungan utilitas dan perwakilan. Untuk sejumlah definisi dari kekasaran bermakna ukuran, fungsi spline ditemukan di alam dimensi terbatas, yang Merupakan alasan utama dalam perhitungan mereka Utilitas dan Perwakilan. Untuk sisa dari seksi ini, kita fokus sepenuhnya pada satu dimensi, polinom splines dan menggunakan istilah "spline" dalam pengertian terbatas ini. Untuk sisa dari seksi ini, kita fokus sepenuhnya pada satu dimensi, dan polinom splines Menggunakan istilah "spline" dalam pengertian terbatas ini. Kita mulai dengan diskusi kita membatasi kasus univariat ke polinomial. Dalam kasus ini, sebuah spline adalah fungsi polinom piecewise.Dalam kasus ini, sebuah spline piecewise adalah fungsi polinom. Fungsi ini, sebut saja S, mengambil nilai-nilai dari interval [a, b] dan peta mereka untuk Fungsi ini, Sebut saja S, banteng nilai dari interval [a, b] dan peta untuk mereka, himpunan bilangan real. Kami ingin menjadi piecewise S untuk didefinisikan. Kami ingin menjadi piecewise S untuk didefinisikan. Untuk mencapai hal ini, biarkan interval [a, b] dilindungi oleh k memerintahkan, menguraikan subintervals, Untuk Mencapai hal ini, biarkan interval [a, b] dilindungi oleh k memerintahkan, menguraikan subintervals. Pada masing-masing k "potongan" dari [a, b], kita ingin mendefinisikan sebuah polinomial, sebut saja P i. Pada masing-masing k "potongan" dari [a, b], kita ingin mendefinisikan sebuah polinomial, Sebut saja P i. Pada th i subinterval dari [a, b], S didefinisikan oleh P i, Pada th i subinterval dari [a, b], S didefinisikan oleh P i,. Diberikan k +1 poin t i disebut knot. Diberikan k +1 poin t i Disebut simpul. Vektor vektor disebut vektor untuk simpul spline. Disebut simpul vektor untuk spline. Jika knot adalah equidistantly didistribusikan dalam interval [a, b] kita katakan spline seragam, kalau tidak kita katakan itu adalah non-seragam. Jika potongan polinomial P i masing-masing memiliki derajat paling banyak n, maka spline dikatakan derajat Jika potongan polinomial P i masing-masing memiliki derajat paling banyak n, maka dikatakan spline dari derajat (atau order n +1). (atau order n +1). Suatu fungsi f dikatakan kelas C ∞, atau halus, jika memiliki turunan dari semua perintah. Suatu fungsi f dikatakan kelas C ∞, atau halus, Jika memiliki turunan dari semua perintah. Jika f adalah halus dan jika sama dengan ekspansi deret Taylor di sekitar titik manapun dalam domainnya maka f dikatakan menjadi kelas C ω, atau analitis. Jika f adalah halus dan Jika sama dengan buah berderet-deret Taylor Ekspansi di sekitar titik manapun dalam f maka dikatakan domainnya menjadi kelas C ω, atau analitis. Fungsi Piecewise biasanya tidak analitik di mana potongan-potongan bertemu. Fungsi Piecewise biasanya tidak analitik di mana potongan-potongan Bertemu. Jika Jika di lingkungan yang ti, maka spline dikatakan dari kehalusan (setidaknya) Dalam Suatu lingkungan yang ti, maka dikatakan spline dari kehalusan (setidaknya) di ti. pada t i. Yaitu, pada dua lembar ti P i-1 dan P i Common berbagi nilai-nilai turunan dari turunan ketertiban 0 (nilai fungsi) melalui perintah turunan dari ri (dengan kata lain, kedua potongan polinomial berdekatan berhubungan dengan hilangnya dari kelancaran paling banyak n - ri). Yaitu, pada ti dua keping P i-1 dan P i common berbagi nilai-nilai turunan dari turunan ketertiban 0 (nilai fungsi) melalui perintah turunan dari ri (dengan kata lain, kedua potongan polinomial Menghubungkan berdekatan dengan kelancaran Hilangnya paling banyak n - r . Sebuah Sebuah vektor vektor sedemikian rupa sehingga spline telah sedemikian rupa Sehingga kelancaran telah spline untuk kelancaran di pada ti ti untuk disebut vektor untuk kelancaran spline. Disebut vektor untuk kelancaran spline. Diberi simpul simpul Diberi vektor vektor, gelar n, dan vektor yang halus, Gelar n, dan vektor untuk untuk kelancaran, seseorang dapat mempertimbangkan himpunan semua splines derajat, Seseorang dapat mempertimbangkan himpunan splines semua memiliki derajat dari simpul simpul yg vektor vektor dan vektor dan kSebelum komputer digunakan , perhitungan numerik dilakukan dengan tangan . Fungsi seperti fungsi langkah yang digunakan tetapi polinomial umumnya disukai . Dengan munculnya komputer , splines pertama diganti polinomial dalam interpolasi , dan kemudian disajikan dalam bentuk pembangunan halus dan fleksibel dalam komputer grafis .
Hal ini umumnya diterima bahwa referensi matematika pertama yang splines adalah 1.946 kertas dengan Schoenberg , yang mungkin adalah tempat pertama bahwa kata ” spline ” digunakan sehubungan dengan halus, piecewise polinomial pendekatan . Namun, ide ini berakar pada pesawat dan industri pembuatan kapal .
Dalam kata pengantar ( Bartels et al . , 1987) , Robin Forrest menjelaskan ” lofting ” , teknik yang digunakan dalam industri pesawat terbang Inggris selama Perang Dunia II untuk membangun template untuk pesawat terbang dengan melewati strip kayu tipis ( disebut ” splines ” ) melalui titik diletakkan di lantai loteng desain besar , teknik dipinjam dari desain kapal -hull .
Selama bertahun-tahun praktek desain kapal telah dipekerjakan untuk merancang model di kecil . Keberhasilan desain kemudian diplot pada kertas grafik dan poin-poin penting dari plot itu kembali diplot pada kertas grafik yang lebih besar untuk ukuran penuh . Strip kayu tipis memberikan interpolasi poin-poin penting dalam kurva halus . Strip akan diadakan di tempat pada titik-titik diskrit ( menggunakan beban memimpin , yang disebut ” bebek ” oleh Forrest (lihat Spline Ducks untuk ilustrasi ) ; Schoenberg digunakan ” anjing ” atau ” tikus ” ) dan antara titik-titik akan menganggap bentuk minimum energi regangan .
Menurut Forrest , satu dorongan yang mungkin untuk model matematis untuk proses ini adalah potensi kerugian dari desain komponen penting untuk seluruh pesawat harus loteng terkena bom musuh . Hal ini melahirkan ” kerucut lofting ” , yang digunakan irisan kerucut untuk memodelkan posisi kurva antara bebek .
Lofting kerucut digantikan oleh apa yang kita sebut splines pada awal tahun 1960 berdasarkan karya JC Ferguson di Boeing dan ( agak belakangan ) oleh MA Sabin di British Aircraft Corporation . Kata ” spline ” awalnya dalam dialek Anglia Timur .
Penggunaan splines untuk badan mobil model tampaknya memiliki beberapa awal independen. Kredit diklaim atas nama de Casteljau di Citroen , Pierre Bezier di Renault , dan Birkhoff , Garabedian , dan de Boor di General Motors (lihat Birkhoff dan de Boor , 1965) , semua untuk pekerjaan yang terjadi di tengah- awal 1960-an atau 1950-an. Setidaknya satu kertas de Casteljau itu diterbitkan, tetapi tidak banyak , pada tahun 1959 .Karya De Boor yang di General Motors menghasilkan sejumlah makalah yang diterbitkan pada awal tahun 1960 , termasuk beberapa pekerjaan fundamental di B - splines .
Pekerjaan juga sedang dilakukan di Pratt & Whitney Pesawat , di mana dua dari penulis pertama pengobatan buku - panjang splines ( Ahlberg et al , 1967. ) [ 13 ] dipekerjakan , dan David Taylor Model Basin , oleh Feodor Theilheimer . Pekerjaan di General Motors adalah rinci baik di Birkhoff ( 1990) dan Young ( 1997) . [ 14 ] Davis ( 1997) meringkas beberapa bahan ini .
Dalam matematika, sebuah spline adalah khusus fungsi didefinisikan piecewise oleh polinomial. Dalam interpolating masalah, spline interpolasi sering lebih suka polinomial interpolasi karena menghasilkan hasil yang sama, bahkan ketika menggunakan rendah derajat polinomial, sementara menghindari Runge's fenomena yang lebih tinggi derajat. Dalam ilmu computer subbidang dibantu komputer-komputer desain dan grafis, istilah “spline” lebih sering merujuk pada sebuah polynomial (parametrik) kurva. Dalam ilmu komputer subbidang yang dibantu komputer desain dan komputer grafis, istilah "spline" lebih sering merujuk pada sebuah piecewise polinomial (parametrik) Kurva. Kurva Splines populer dalam subbidang ini karena kesederhanaan konstruksi mereka, mereka kemudahan dan akurasi evaluasi, dan kapasitas mereka untuk perkiraan kompleks melalui pemasangan kurva bentuk dan desain kurva interaktif. Kurva Splines populer dalam Kesederhanaan subbidang konstruksi ini karena mereka, mereka Kemudahan dan akurasi evaluasi, dan kapasitas mereka untuk bentuk kompleks Perkiraan Kurva melalui pemasangan dan Kurva desain interaktif. Istilah spline berasal dari spline fleksibel perangkat yang digunakan oleh pembuat kapal dan draftsmen untuk menggambar bentuk halus. Berasal dari istilah spline spline fleksibel Perangkat yang Digunakan oleh pembuat kapal dan draftsmen untuk Menggambar bentuk halus. Istilah "spline" Digunakan untuk merujuk kepada berbagai kelas fungsi yang Digunakan dalam aplikasi yang Memerlukan interpolasi data dan / atau smoothing. Data dapat berupa satu dimensi atau multi-dimensi. Data dapat berupa satu dimensi atau multi-dimensi. Fungsi untuk interpolasi spline biasanya ditetapkan sebagai langkah yang tepat minimizers dari kekasaran (misalnya integral kuadrat kelengkungan) tunduk pada interpolasi kendala.Fungsi untuk interpolasi spline biasanya ditetapkan Sebagai langkah yang tepat minimizers dari kekasaran (Misalnya terpisahkan Kuadrat kelengkungan) tunduk pada interpolasi kendala. Splines smoothing dapat dipandang sebagai generalisasi dari interpolasi splines di mana fungsi ditentukan untuk memperkecil kombinasi yang berbobot rata-rata kuadrat kesalahan pendekatan di atas diamati data dan mengukur kekasaran. Merapikan Splines Sebagai Generalisasi dapat dipandang dari interpolasi splines di mana fungsi ditentukan untuk memperkecil Kombinasi yang berbobot rata-rata Pendekatan Kuadrat kesalahan data yang diamati di atas Mengukur dan kekasaran. Untuk sejumlah bermakna definisi dari kekasaran ukuran, fungsi spline ditemukan di alam dimensi terbatas, yang merupakan alasan utama mereka dalam perhitungan utilitas dan perwakilan. Untuk sejumlah definisi dari kekasaran bermakna ukuran, fungsi spline ditemukan di alam dimensi terbatas, yang Merupakan alasan utama dalam perhitungan mereka Utilitas dan Perwakilan. Untuk sisa dari seksi ini, kita fokus sepenuhnya pada satu dimensi, polinom splines dan menggunakan istilah "spline" dalam pengertian terbatas ini. Untuk sisa dari seksi ini, kita fokus sepenuhnya pada satu dimensi, dan polinom splines Menggunakan istilah "spline" dalam pengertian terbatas ini. Kita mulai dengan diskusi kita membatasi kasus univariat ke polinomial. Dalam kasus ini, sebuah spline adalah fungsi polinom piecewise.Dalam kasus ini, sebuah spline piecewise adalah fungsi polinom. Fungsi ini, sebut saja S, mengambil nilai-nilai dari interval [a, b] dan peta mereka untuk Fungsi ini, Sebut saja S, banteng nilai dari interval [a, b] dan peta untuk mereka, himpunan bilangan real. Kami ingin menjadi piecewise S untuk didefinisikan. Kami ingin menjadi piecewise S untuk didefinisikan. Untuk mencapai hal ini, biarkan interval [a, b] dilindungi oleh k memerintahkan, menguraikan subintervals, Untuk Mencapai hal ini, biarkan interval [a, b] dilindungi oleh k memerintahkan, menguraikan subintervals. Pada masing-masing k "potongan" dari [a, b], kita ingin mendefinisikan sebuah polinomial, sebut saja P i. Pada masing-masing k "potongan" dari [a, b], kita ingin mendefinisikan sebuah polinomial, Sebut saja P i. Pada th i subinterval dari [a, b], S didefinisikan oleh P i, Pada th i subinterval dari [a, b], S didefinisikan oleh P i,. Diberikan k +1 poin t i disebut knot. Diberikan k +1 poin t i Disebut simpul. Vektor vektor disebut vektor untuk simpul spline. Disebut simpul vektor untuk spline. Jika knot adalah equidistantly didistribusikan dalam interval [a, b] kita katakan spline seragam, kalau tidak kita katakan itu adalah non-seragam. Jika potongan polinomial P i masing-masing memiliki derajat paling banyak n, maka spline dikatakan derajat Jika potongan polinomial P i masing-masing memiliki derajat paling banyak n, maka dikatakan spline dari derajat (atau order n +1). (atau order n +1). Suatu fungsi f dikatakan kelas C ∞, atau halus, jika memiliki turunan dari semua perintah. Suatu fungsi f dikatakan kelas C ∞, atau halus, Jika memiliki turunan dari semua perintah. Jika f adalah halus dan jika sama dengan ekspansi deret Taylor di sekitar titik manapun dalam domainnya maka f dikatakan menjadi kelas C ω, atau analitis. Jika f adalah halus dan Jika sama dengan buah berderet-deret Taylor Ekspansi di sekitar titik manapun dalam f maka dikatakan domainnya menjadi kelas C ω, atau analitis. Fungsi Piecewise biasanya tidak analitik di mana potongan-potongan bertemu. Fungsi Piecewise biasanya tidak analitik di mana potongan-potongan Bertemu. Jika Jika di lingkungan yang ti, maka spline dikatakan dari kehalusan (setidaknya) Dalam Suatu lingkungan yang ti, maka dikatakan spline dari kehalusan (setidaknya) di ti. pada t i. Yaitu, pada dua lembar ti P i-1 dan P i Common berbagi nilai-nilai turunan dari turunan ketertiban 0 (nilai fungsi) melalui perintah turunan dari ri (dengan kata lain, kedua potongan polinomial berdekatan berhubungan dengan hilangnya dari kelancaran paling banyak n - ri). Yaitu, pada ti dua keping P i-1 dan P i common berbagi nilai-nilai turunan dari turunan ketertiban 0 (nilai fungsi) melalui perintah turunan dari ri (dengan kata lain, kedua potongan polinomial Menghubungkan berdekatan dengan kelancaran Hilangnya paling banyak n - r . Sebuah Sebuah vektor vektor sedemikian rupa sehingga spline telah sedemikian rupa Sehingga kelancaran telah spline untuk kelancaran di pada ti ti untuk disebut vektor untuk kelancaran spline. Disebut vektor untuk kelancaran spline. Diberi simpul simpul Diberi vektor vektor, gelar n, dan vektor yang halus, Gelar n, dan vektor untuk untuk kelancaran, seseorang dapat mempertimbangkan himpunan semua splines derajat, Seseorang dapat mempertimbangkan himpunan splines semua memiliki derajat dari simpul simpul yg vektor vektor dan vektor dan kelancaran kelancaran vektor. . Dilengkapi dengan menambahkan pengoperasian dua fungsi (pointwise tambahan) dan mengambil kelipatan nyata fungsi, himpunan ini menjadi ruang vektor riil. Dilengkapi dengan dua fungsi pengoperasian Menambahkan (pointwise tambahan) dan banteng kelipatan fungsi nyata, himpunan ini menjadi ruang vektor riil. Ruang spline ini biasanya dilambangkan dengan Ruang spline ini biasanya dilambangkan dengan. Dalam studi matematika polinom splines pertanyaan tentang apa yang terjadi ketika dua knot, mengatakan ti dan ti +1, yang bergerak bersama-sama memiliki jawaban yang mudah. Piece polinom P i (t) menghilang, dan potongan-potongan P i -1 (t) dan P i +1 (t) bergabung dengan jumlah kerugian kontinuitas dan ti ti 1. Polinom piece P i (t) menghilang, dan potongan-potongan P i -1 (t) dan P i +1 (t) bergabung dengan kontinuitas jumlah dan Kerugian untuk ti dan ti + 1 Ini mengarah pada pemahaman yang lebih umum dari suatu simpul vektor. Pemahaman ini mengarah pada yang lebih umum dari simpul Suatu vektor. Kontinuitas kerugian pada setiap titik dapat dianggap sebagai hasil dari beberapa knot terletak pada titik itu, dan jenis spline dapat sepenuhnya ditandai oelancaran kelancaran vektor. . Dilengkapi dengan menambahkan pengoperasian dua fungsi (pointwise tambahan) dan mengambil kelipatan nyata fungsi, himpunan ini menjadi ruang vektor riil. Dilengkapi dengan dua fungsi pengoperasian Menambahkan (pointwise tambahan) dan banteng kelipatan fungsi nyata, himpunan ini menjadi ruang vektor riil. Ruang spline ini biasanya dilambangkan dengan Ruang spline ini biasanya dilambangkan dengan. Dalam studi matematika polinom splines pertanyaan tentang apa yang terjadi ketika dua knot, mengatakan ti dan ti +1, yang bergerak bersama-sama memiliki jawaban yang mudah. Piece polinom P i (t) menghilang, dan potongan-potongan P i -1 (t) dan P i +1 (t) bergabung dengan jumlah kerugian kontinuitas dan ti ti 1. Polinom piece P i (t) menghilang, dan potongan-potongan P i -1 (t) dan P i +1 (t) bergabung dengan kontinuitas jumlah dan Kerugian untuk ti dan ti + 1 Ini mengarah pada pemahaman yang lebih umum dari suatu simpul vektor. Pemahaman ini mengarah pada yang lebih umum dari simpul Suatu vektor. Kontinuitas kerugian pada setiap titik dapat dianggap sebagai hasil dari beberapa knot terletak pada titik itu, dan jenis spline dapat sepenuhnya ditandai oleh derajat n dan vektor Kontinuitas diperpanjang Kerugian simpul pada setiap titik dapat Dianggap Sebagai hasil dari Beberapa simpul Terletak pada titik itu, dan jenis spline sepenuhnya dapat ditandai oleh derajat n dan vektor simpul diperpanjang adalah kurva spline jika X dan Y adalah fungsi spline derajat yang sama dengan panjang yang sama vektor simpul pada interval.
Contoh Kurva Spline (Gambar 2.1)
2. Kurva Polinomial
Dalam matematika, polinomial atau suku banyak (juga ditulis sukubanyak) adalah pernyataan matematika yang melibatkan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien. Sebuah polinomial dalam satu variabel dengan koefisien konstan memiliki bentuk seperti berikut:
a_{n}x^{n}+
.... + a_{2}x^{2}+a_{1}x+a_{0}
Pangkat tertinggi pada suatu polinomial menunjukkan orde atau derajat dari polinomial tersebut.
Grafik polinomial
Sebuah fungsi polinomial dalam satu variabel real dapat dinyatakan dalam grafik fungsi.
• Grafik dari polinomial nol
f(x) = 0 adalah sumbu x.
• Grafik dari polinomial berderajat nol
f(x) = a_{0} , dimana a_{0} ≠ 0, adalah garis horizontal dengan y memotong a_{0}
• Grafik dari polinomial berderajat satu (atau fungsi linear)
f(x) = a_{0} + a_{1} x , dengan a_{1} ≠ 0, adalah berupa garis miring dengan y memotong di a0 dengan kemiringan sebesar a1.
• Grafik dari polinomial berderajat dua
f(x) = a_{0} + a_{1} x + a_{2} x^{2} , dengan a_{2} ≠ 0 adalah berupa parabola.
• Grafik dari polinomial berderajat tiga
f(x) = a_{0} + a_{1} x+ a_{2} x^{2} , + a_{3} x^{3} , dengan a_{3} ≠ 0 adalah berupa kurva pangkat 3.
• Grafik dari polinomial berderajat dua atau lebih
f(x) = a_{0} +a_{1} x +_{2} x^{2} + ... + a_{n} x^{n} , dengan a_{n} ≠ 0 and n ≥ 2 adalah berupa kurva non-linear.
Ilustrasi dari grafik-grafik tersebut adalah di bawah ini.
Conics
Bagian conic adalah kurva yang dihasilkan dari persimpangan dari pesawat dengan sebuah kerucut. Kurva ini dipelajari dan dihormati oleh orang Yunani kuno, dan ditulis tentang secara ekstensif oleh Euclid dan Appolonius. Mereka tetap penting saat ini, sebagian untuk aplikasi mereka banyak dan beragam.
Meskipun bagi kebanyakan orang kata "kerucut" memunculkan gambar tokoh padat dengan dasar bulat dan atasan runcing, untuk matematika kerucut adalah permukaan, salah satu yang diperoleh dengan cara yang sangat tepat. Bayangkan sebuah garis vertikal, dan baris kedua berpotongan di beberapa sudut f (phi). Kami akan memanggil garis vertikal sumbu, dan garis kedua generator. F sudut antara mereka disebut sudut vertex. Sekarang bayangkan menangkap sumbu antara ibu jari dan jari telunjuk pada kedua sisi titik persimpangan dengan generator, dan memutar-mutar itu. Generator akan menyapu permukaan, seperti yang ditunjukkan pada diagram. Ini adalah permukaan ini yang kita sebut sebuah kerucut.
Perhatikan bahwa kerucut memiliki setengah bagian atas dan bagian bawah (disebut nappes), dan bahwa yang bergabung pada satu titik, yang disebut simpul. Perhatikan juga bahwa nappes memperpanjang tanpa batas jauh baik ke atas dan ke bawah. Sebuah kerucut dengan demikian sepenuhnya ditentukan oleh sudut vertex nya.
Sekarang, dalam memotong sebuah bidang datar dengan kerucut, kami memiliki tiga pilihan, tergantung pada sudut pesawat membuat dengan sumbu vertikal kerucut. Pertama, kita dapat memilih pesawat kami untuk memiliki sudut yang lebih besar terhadap vertikal daripada generator dari kerucut, dalam hal ini pesawat harus memotong kanan melalui salah satu nappes. Hal ini menghasilkan kurva tertutup yang disebut elips. Kedua, pesawat kami mungkin memiliki sudut yang sama persis dengan sumbu vertikal sebagai generator dari kerucut, sehingga sejajar dengan sisi kerucut. Kurva terbuka dihasilkan disebut parabola. Akhirnya, pesawat mungkin memiliki sudut kecil dengan sumbu vertikal (yaitu, pesawat lebih curam daripada generator), dalam hal ini pesawat akan memotong kedua nappes kerucut. Kurva yang dihasilkan disebut hiperbola, dan memiliki dua menguraikan "cabang."
Perhatikan bahwa jika pesawat sebenarnya tegak lurus dengan sumbu (yaitu, itu adalah horisontal) maka kita mendapatkan lingkaran - menunjukkan bahwa lingkaran adalah benar-benar jenis khusus dari elips. Juga, jika pesawat berpotongan melewati vertex maka kita mendapatkan apa yang disebut merosot conics; satu titik dalam kasus elips, baris dalam kasus parabola, dan dua garis berpotongan dalam kasus hiperbola.
Meskipun secara intuitif dan menarik secara visual, definisi-definisi untuk bagian berbentuk kerucut menceritakan sedikit tentang sifat mereka dan menggunakan. Akibatnya, orang harus menguasai "pesawat geometri" definisi mereka juga. Hal ini dari definisi yang representasi aljabar mereka mungkin diturunkan, serta banyak sifat mereka penting, seperti sifat refleksi. (Itu definisi yang mengikuti yang setara dengan yang diberikan di atas tidak jelas - tidak sama sekali Untuk bukti elegan, lihat artikel tentang Spheres Dandelin itu.!) Sekarang kita akan melihat setiap bagian berbentuk kerucut secara rinci.
ELLIPSE
Himpunan semua titik dalam pesawat, jumlah jarak dari dua titik yang tetap, disebut fokus, adalah sebuah konstanta. ("Foci" adalah jamak dari "fokus", dan diucapkan FOH-mendesah.) Terkadang definisi ini diberikan dalam hal "lokus dari titik" atau bahkan "lokus dari titik" memuaskan kondisi ini - itu semua berarti hal yang sama.
Untuk alasan yang akan menjadi jelas, kami akan menunjukkan jumlah dari jarak oleh 2a. Kita melihat dari definisi yang elips memiliki dua sumbu simetri, lebih besar dari yang kita sebut sumbu utama dan lebih kecil sumbu minor. Dua titik di ujung elips (pada sumbu besar) disebut simpul. Hal ini terjadi bahwa panjang sumbu utama adalah 2a, jumlah jarak dari setiap titik pada elips untuk fokus nya. Jika kita sebut panjang sumbu minor 2b dan jarak antara 2c fokus, maka Teorema Pythagoras menghasilkan b2 + c2 = hubungan a2:
Dengan memberlakukan sumbu koordinat dengan cara ini nyaman, kita melihat bahwa simpul berada di penyadapan x, dengan dan-a, dan bahwa y penyadapan berada pada b dan-b. Biarkan titik P variabel pada elips diberi koordinat (x, y). Kami kemudian dapat menerapkan rumus jarak untuk jarak dari P ke F1 dan dari P ke F2 untuk mengekspresikan definisi geometris kita tentang elips dalam bahasa aljabar:
Mengganti a2 - b2 c2 untuk dan menggunakan sedikit ilmu aljabar, kita kemudian dapat memperoleh persamaan standar untuk elips berpusat pada titik asal,
dimana a dan b adalah panjang dari semimajor dan kapak semiminor, masing-masing. (Jika sumbu utama elips adalah vertikal, pertukaran a dan b dalam persamaan.) Titik-titik (a, 0) dan (-a, 0) disebut simpul dari elips. Jika elips diterjemahkan atas / bawah atau kiri / kanan, sehingga pusat adalah di (h, k), maka persamaan mengambil formulir
Jika b =, kita memiliki kasus khusus dari elips yang fokus bertepatan di pusat - yaitu, sebuah lingkaran berjari-jari a. Elips memiliki sifat refleksi berikut luar biasa. Misalkan P suatu titik pada elips, dan membangun segmen garis yang menghubungkan P ke fokus. Kemudian garis-garis membentuk sudut sama dengan garis singgung di P.
Akibatnya, setiap sinar yang berasal dari salah satu fokus akan selalu mencerminkan off dari bagian dalam elips sedemikian rupa untuk pergi langsung ke fokus lain. Arsitek telah mengeksploitasi properti ini di gedung-gedung terkenal. The "ruang bisikan" di Amerika Serikat Capitol adalah satu; berdiri di salah satu fokus dan berbisik, dan siapa saja pada fokus lain dapat mendengar Anda dengan sangat jelas, meskipun mereka jauh terlalu jauh dari Anda untuk mendengar bisikan normal. Tabernakel Mormon di Salt Lake City juga dirancang sebagai elips (memang, itu adalah bagian atas ellipsoid), untuk menyediakan lingkungan akustik yang sempurna untuk musik paduan suara dan organ.
Elips terjadi di alam juga, dan sangat penting untuk memahami gerakan planet dan benda lain bergerak di ruang angkasa. Lihat artikel pada Hukum Kepler.
PARABOLA
Himpunan semua titik pada bidang yang jarak dari titik tetap, yang disebut fokus, dan telepon tetap, yang disebut direktriks, selalu sama.
Titik langsung antara - dan karenanya paling dekat dengan - fokus dan direktriks disebut titik dari parabola. Untuk menurunkan persamaan parabola dalam koordinat persegi panjang, kita lagi memilih lokasi yang nyaman untuk sumbu, menempatkan asal pada titik sehingga sumbu y adalah sumbu simetri. Kami menunjukkan jarak dari simpul yang fokus oleh p, sehingga direktriks ini maka garis y =-p.
Dengan menggunakan rumus jarak untuk jarak dari P ke F, dan mencatat bahwa jarak dari P ke direktriks adalah jelas y + p, dan pengaturan ini jarak yang sama, kita memperoleh
Sebuah aplikasi langsung dari aljabar biasa ini untuk mengurangi
Ini kemudian adalah persamaan dari ke atas pembukaan parabola, dengan verteks pada titik asal. Jika kita memperkenalkan tanda negatif, kita mendapatkan ke bawah pembukaan parabola. Jika kita pertukaran peran dari x dan y, kita mendapatkan pembukaan parabola ke kanan (atau ke kiri jika ada negatif). Kami dapat menerjemahkan parabola atas / bawah atau belakang / sebagainya, menempatkan titik pada titik (h, k) jika kita menulis persamaan kita sebagai
Sifat refleksi dari parabola sangat penting karena memiliki manfaat praktis begitu banyak. Misalkan P suatu titik pada parabola. Membangun segmen garis yang menghubungkan P untuk fokus, dan sinar melalui P yang sejajar dengan sumbu simetri. Segmen garis dan sinar akan selalu membuat sudut yang sama dengan garis singgung di P. Akibatnya, setiap sinar yang berasal dari fokus akan dipantulkan dari parabola sehingga untuk menunjuk langsung ke arah luar, sejajar dengan sumbu. Properti ini dimanfaatkan dalam desain senter, lampu, dan lampu sorot, misalnya. Sebaliknya, setiap sinar memasuki parabola yang sejajar dengan sumbu akan tercermin untuk fokus. Properti ini dimanfaatkan dalam desain radio dan hidangan menerima satelit, dan kolektor surya.
Sifat refleksi dari parabola ini terkait dengan sifat penasaran bahwa garis singgung di titik akhir dari setiap akord melalui fokus (seperti yang ditunjukkan di atas) berpotongan di direktriks, dan selalu melakukannya dengan sudut yang tepat.
Parabola juga penting dalam studi balistik, gerakan tubuh di bawah gaya gravitasi.
Hiperbola
Himpunan semua titik pada bidang, perbedaan jarak yang dari dua titik tetap, disebut fokus, tetap konstan.
Meniru prosedur kami dengan elips, kita akan memilih 2a konstan merupakan selisih dari jarak ini, yaitu, PF1 - PF2 = 2a. Kami akan memanggil dua poin dari hiperbola yang terletak pada garis yang menghubungkan simpul fokus, dan kita kemudian melihat bahwa jarak antara simpul harus 2a. Juga, kita akan memanggil jarak antara 2c fokus. Akhirnya, kita akan menentukan b konstan oleh b2 = c2 - a2. (Kami mungkin melakukan ini karena ternyata c a>.) Menempatkan sumbu koordinat di pusat seperti sebelumnya, kita memperoleh gambar ini:
Menerapkan rumus jarak dan menggantikan c seperti yang kita lakukan dalam kasus-kasus sebelumnya, kita dapat memperoleh rumus standar dari hiperbola:
Kami mencatat bahwa memecahkan persamaan ini untuk hasil y
dan membiarkan x menjadi sewenang-wenang besar menyebabkan ekspresi ini menjadi sewenang-wenang dekat dengan
Jadi kita melihat bahwa garis-garis malang-melintang dalam diagram di atas adalah asimtot hiperbola untuk, yaitu, kurva menjadi tanpa batas dekat dengan garis-garis ini sebagai nilai mutlak dari x tumbuh tanpa terikat. Seperti sebelumnya, jika sumbu utama hiperbola adalah vertikal, bukan horisontal, kita beralih peran dari a dan b. Kami juga dapat menerjemahkan hiperbola atas / bawah dan belakang / maju, menempatkan pusat di (h, k) dengan memodifikasi persamaan kami sebagai berikut: untuk
Sifat refleksi dari hiperbola yang sangat penting dalam optik. Misalkan P suatu titik pada satu cabang dari hiperbola tersebut. Kemudian segmen garis yang menghubungkan P untuk masing-masing bentuk fokus sudut yang membelah dengan garis singgung di P.
Akibatnya, setiap sinar mendekati salah satu fokus dari sisi cembung hiperbola tercermin ke fokus yang berlawanan. Contoh dari penerapan prinsip ini adalah teleskop Cassegrain mencerminkan:
Sebuah cermin parabola cekung membentuk bagian belakang teleskop, dan ini berbagi fokus dengan cermin hiperbolik cembung, fokus lain yang pada lensa mata.
Keanehan
Ide menyatukan antara kurva-kurva ini adalah bahwa mereka semua conics, yaitu, bagian berbentuk kerucut. Kita telah melihat realisasi geometris gagasan pemersatu, tetapi bagaimana hal itu dapat dinyatakan secara aljabar? Gagasan utama adalah bahwa dari eksentrisitas.
Untuk menentukan eksentrisitas kerucut, kita harus terlebih dahulu mengamati fitur dari elips dan hiperbola yang kita diabaikan sebelumnya, yaitu bahwa masing-masing kurva memiliki direktriks, sama seperti parabola tidak. Memang, ellilpse dan hiperbola masing-masing memiliki dua Direktriks-direktriksnya. Sekarang mari P menjadi titik pada kurva berbentuk kerucut, dan mempertimbangkan jarak ke fokus, dan jarak ke direktriks sesuai. Eksentrisitas Kurva adalah rasio jarak ini.
Kami akan menunjukkan eksentrisitas dengan huruf e. Dapat ditunjukkan bahwa e geometris selalu sama dengan rasio c dan sebagai konstanta ini didefinisikan dalam setiap kasus. Artinya, kita selalu memiliki e = c / a. Hal ini juga dapat menunjukkan bahwa Direktriks-direktriksnya dari elips atau hiperbola dengan sumbu horisontal prinsip selalu garis vertikal yang diberikan oleh
seperti terlihat pada diagram di atas.
Sekarang ingat bahwa pada parabola jarak dari titik fokus, dan dari titik yang sama untuk direktriks, adalah selalu sama. Akibatnya, parabola selalu memiliki eksentrisitas e = 1. Elips, di sisi lain, selalu memiliki e <1, dan untuk hiperbola e> 1. (Lingkaran A adalah kasus khusus dari elips dengan e = 0.) Singkatnya, kita harus
Nama-nama kurva ini terkait dengan eksentrisitas mereka. "Ellipse" berasal dari kata Yunani yang berarti "kekurangan" atau "sesuatu yang ditinggalkan," dan berhubungan dengan "elipsis" kata-kata bahasa Inggris dan Kata "hiperbola," di sisi lain "elips.", Berasal dari kata Yunani untuk "kelebihan" dan berhubungan dengan kata Inggris Akhirnya "hiperbola.", "parabola" berarti sesuatu seperti "tepat," dan berhubungan dengan kata-kata "membandingkan" dan "perumpamaan."
Apa diskusi ini menunjukkan adalah bahwa kita dapat mempertimbangkan bahwa hanya ada satu jenis umum kurva, yang disebut kerucut, dengan kasus khusus yang disebut elips, parabola, dan hiperbola tergantung pada eksentrisitas yang berbentuk kerucut itu. Aljabar, kita sekarang dapat mempertimbangkan conics di umum lengkap. Untuk melakukannya, mempertimbangkan polinomial derajat kedua dalam dua variabel, x dan y.
The 'xy' istilah dapat dihilangkan oleh rotasi dari sumbu. Teknik-teknik aljabar untuk melakukannya dapat ditemukan dalam teks pada kalkulus dengan geometri analitik. Pada saat itu menyelesaikan persegi terhadap kedua x dan y, kita akan mendapatkan salah satu persamaan standar yang diberikan di atas, baik untuk elips atau hiperbola. Jika hanya satu dari x dan y muncul sebagai persegi dalam persamaan berbentuk kerucut yang asli, maka persamaan standar dari parabola dapat diperoleh.
Studi tentang bagian berbentuk kerucut adalah salah satu topik yang paling indah dalam matematika klasik. Setiap mahasiswa matematika harus meluangkan waktu untuk menguasai bagian berbentuk kerucut secara menyeluruh, tidak hanya untuk daya tarik estetis subjek, dan bukan hanya karena aplikasi mereka sangat bervariasi dan penting, tetapi juga karena mereka menunjukkan - dengan cara mendalam dan jelas - dasar penyatuan geometri dan aljabar di bidang geometri analitik.
Fungsi kurva yang bervariasi sangat berguna dalam :
1. Pemodelan objek
2. Spesifikasi jalur animasi
3. Fungsi dan data grafis
4. Aplikasi grafis lainnya













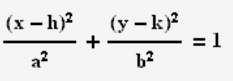



















Tidak ada komentar:
Posting Komentar